The Reality of Math

Posted Aug 19, 2010

---

Math is an important tool, but it often trips us up, instead of helps us. The reason is simple: There are facts in math we are aware of, yet they are so simple and obvious we ignore them. The problem is that which we ignore becomes invisible, and has the potential to trip us up.

Here's an example:

1

The simple number one I just wrote is actually mathematical shorthand. Can you take a piece of paper and write out the longhand version for the number one?

I'll give you some time.

.
.
.
.
.
.
.
.

Still working on it?

.
.
.
.
.
.
.
.

Time's almost up.

.
.
.
.
.
.
.
.

And the answer is:


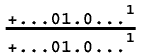
Or in words, positive infinite zeros one, point infinite zeros to the first power, over positive infinite zeros one, point infinite zeros to the first power.

The positive sign, leading and trailing zeros, etc. decimal point, fraction bar and power are all known aspects of math. They are assumed there when we need them. (For example 10 divided by 3)


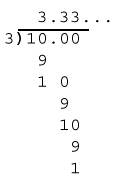
The decimal point & trailing zeros came into effect when we had to go past the main number. Until that need occurs, we don't bother with them. We ignore them.

We obviously can't write every single number in the long version I showed above. That would be ridiculous, silly and overall, useless.

So, we understand those things are there, and ignore them until they are needed.

The problem occurs when we forget to use the information we ignored.

Which leads us to our next point: Mathematical anomalies.

Basic fact of math: Add & subtract the same amount and you get your original amount. Multiply and divide by the same rule and again, the original amount appears.

1+3-3=1
17x12/12=17

But what about 10/3? As shown above
10/3=3.333...
But
3.333...x3=9.999...

So does 9.999... = 10?

This would also mean 0.999...=1 and 99.999...=100, etc., etc.

If you look, you'll find mathematical and logistical proofs both for, and against this phenomenon. People love to debate this funny little abnormality.

However, essentially all of them are missing one of the most obvious, and invisible fact of math that, if remembered and seen, would stop everyone from tripping over this issue.

The fact is simply this: We use a base-10 math system.

This fact, if understood correctly, reminds us that our math system is simply a system, and as such, is capable of quarks, flaws, and glitches in the matrix.

Do any of you know why we use a base-10 math system? Raise your hand if you do.

Well actually, if you raise both hands, you'll get a big hint.

Ten fingers. Ten numbers.

The Base-10 system looks like this:

1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 0

But imagine if we evolved with hands like this:

(Only much better developed, but you get the idea.)

Then we would likely have used a base-6 math system.

1 - 2 - 3 - 4 - 5 - 0

So our numbering would look like: 1, 2, 3, 4, 5, 10, 11, 12, 13, 14, 15, 20, 21, etc., etc.

So, now let's use our new base-6 math, and see what happens.



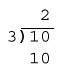
Well lookie what we have.

10/3=2
3x2=10

and everything is right with the world again. No strange 3.333... problems to mess with.

I'm sorry, what? What's that you say?

Oh, you noticed the trick? Well, bravo.

Yes, the above example has a slight flaw: The numeral "10" is actually the numeral "6". Instead of 10/3 we just did 6/3, which in either math system is not a problem.

So, let's redo the math with base-6's equivalent of 10. So let's count it out.

1-2-3 (1-2-3 in base-10)
4-5-10 (4-5-6)
11-12-13 (7-8-9)
14 (10)

So base-6s version of 10 is 14. Let's do the math.



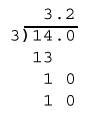
So in base-6 14/3=3.2 and 3.2x3=14

Regardless how we do it, the sticky issue in base-10 is smoothed out in this alternative numeric system. Of course a base-6 math system has its own unique problems, just as a base-10 does, but hopefully you get the idea.

There are plenty of base-numeral math systems we can use, but sticking with the base-10 for everyone makes it a lot easier for everyone to check each others work.

The trick to understanding math, and more importantly, Reality, is to make sure we do not accidentally trip on those obvious things we ignore, nor that we get caught up in accidental, nor deliberate sleight of hand."

Back to list